[과천중앙고] 1학년 2학기 기말고사 고난도 문항 손풀이
안녕하세요. 어수강 박사입니다.
오늘은 "[과천중앙고] 2023년 1학년 2학기 기말고사 고난도 문항 손풀이를 포스팅" 하도록 하겠습니다.
먼저 17번 문항입니다.


박스의 두 번째 조건을 기준으로 경우 나누기를 하면 되겠죠? 이후 박스의 첫 번째 조건과 세 번째 조건을 만족하는지 확인하면 될 것 같네요. 구체적인 풀이는 다음과 같습니다!
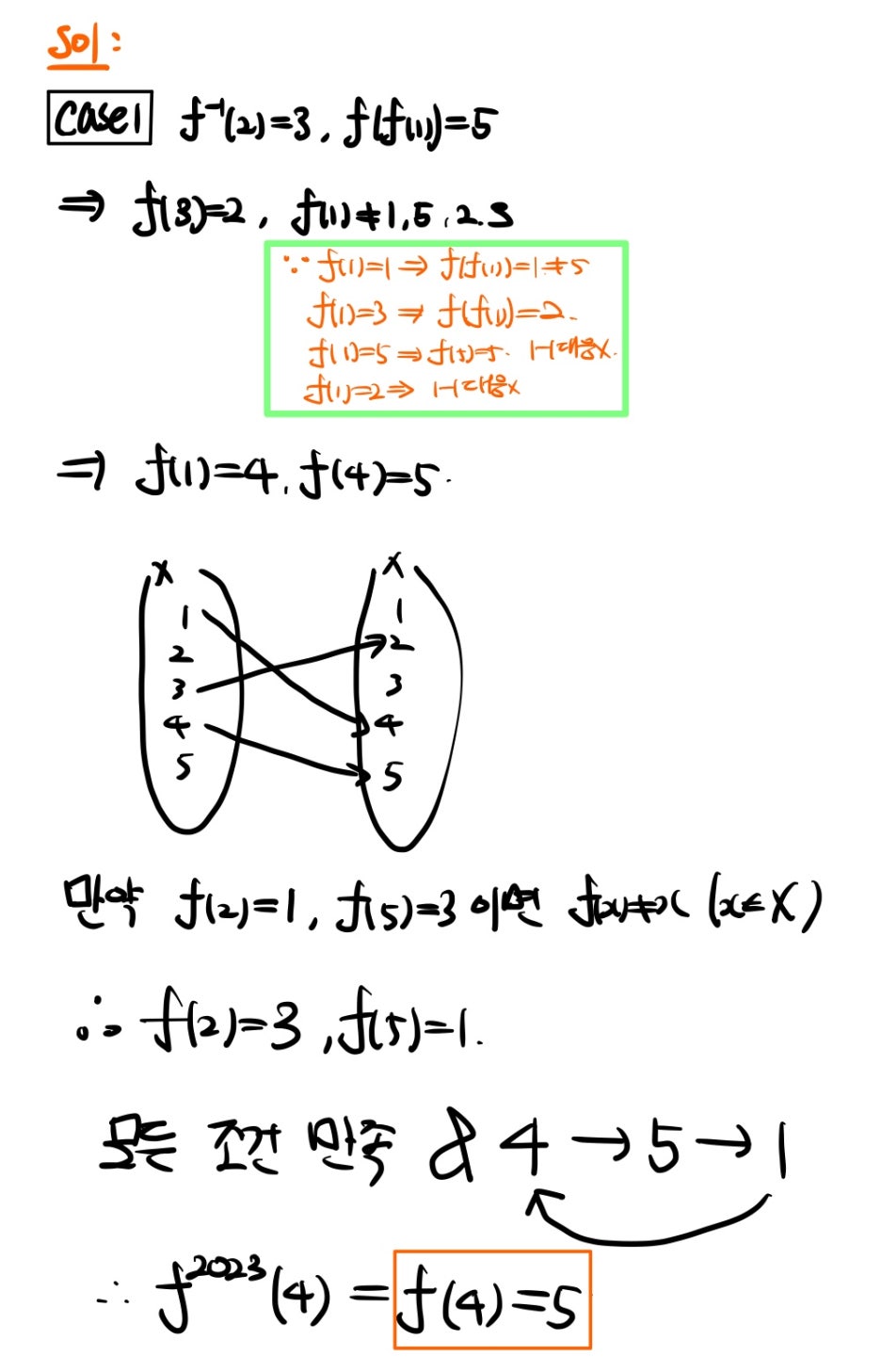

별로 어렵지 않죠? 답은 나왔지만~ Case2도 마저 생각해 볼게요!
(시험에서 case1, case2의 순서가 뒤바뀔 수도 있으니까요 ㅎㅎ)


.
다음은 18번 문항입니다.


대수적으로 풀기 어렵다면 기하적으로 풀면 되겠죠? 함수 y=f(x)의 개형을 그리는 것으로 시작하면 될 것 같습니다.
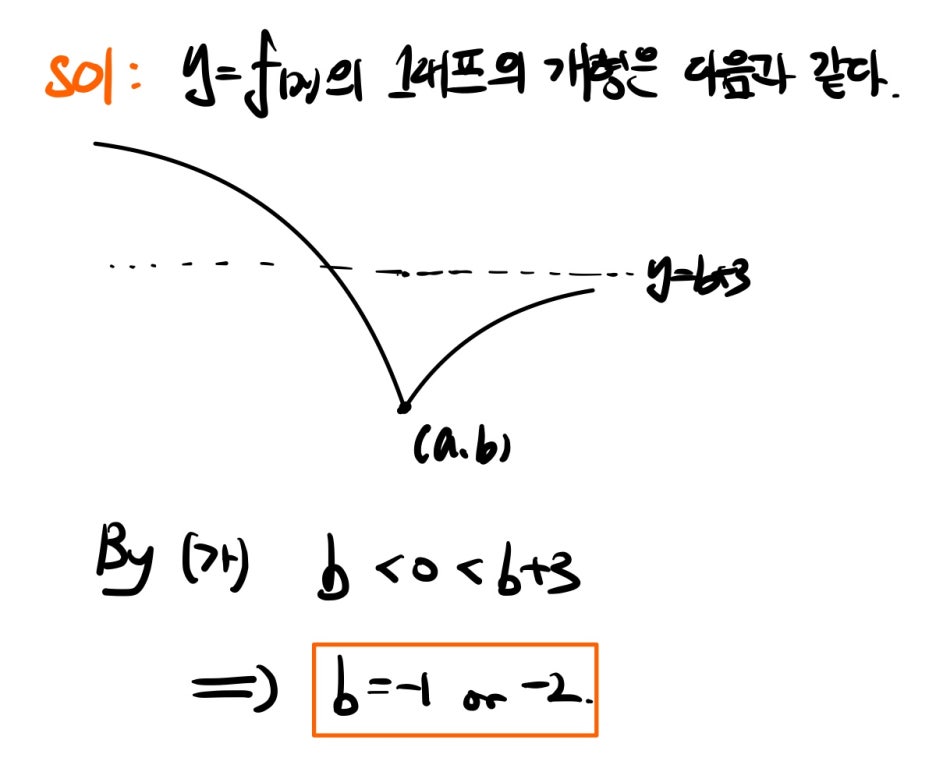

이제 b의 값에 따라 경우를 나누어 풀면 되겠네요! ㅎㅎ 먼저 b=-1인 경우는 다음과 같습니다.
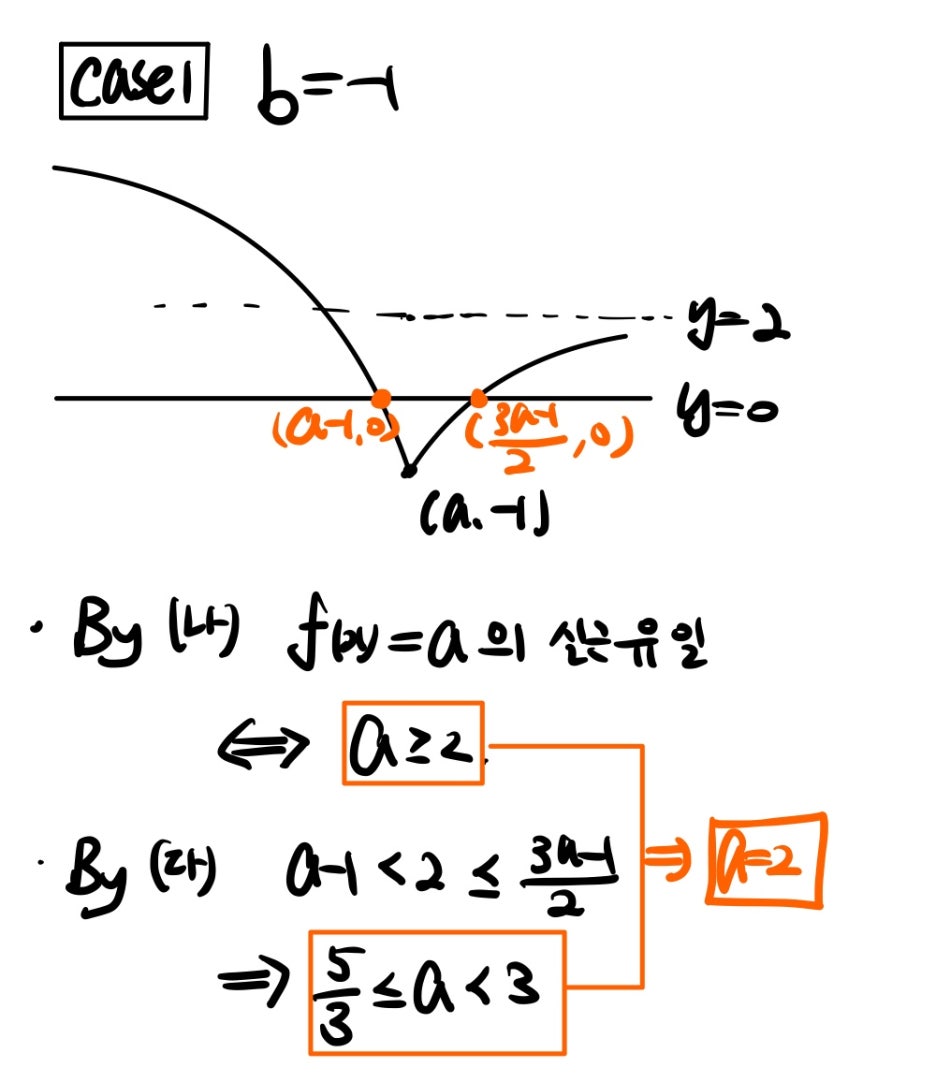

이제 b=-2인 경우만 생각하면 되겠죠?


따라서 답은 다음과 같습니다.

마지막으로 논술형 4번입니다.


복잡해 보이지만 차근차근 풀면 별 거 아니니 쫄지 마세요!ㅎㅎ
저는 조건 (가), (라), (나) 순으로 풀었지만, 순서는 별로 중요하지 않습니다. 하나하나 차근차근 풀기만 하면 됩니다!
저의 풀이는 다음과 같습니다. (참고로 조건 (다)는 쓸모가 없습니다. 왜 저런 조건을 줬을까요?^^;;)
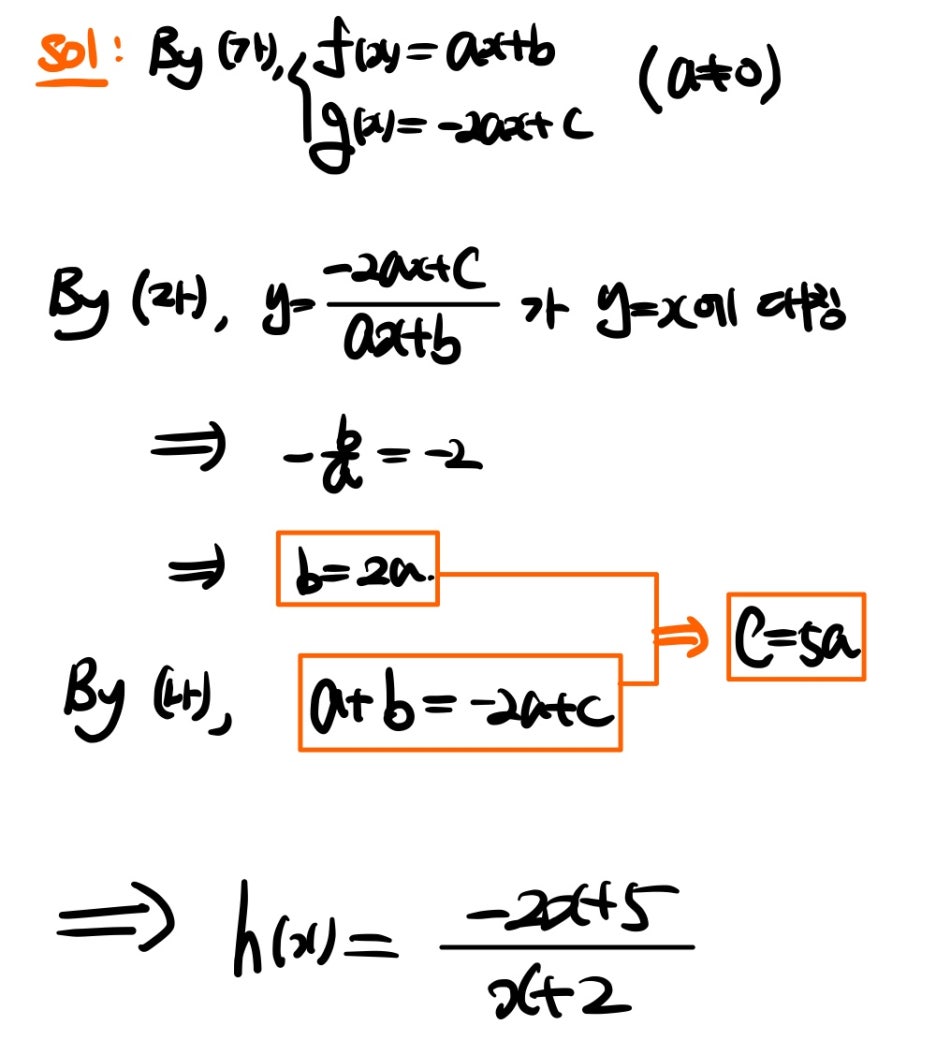

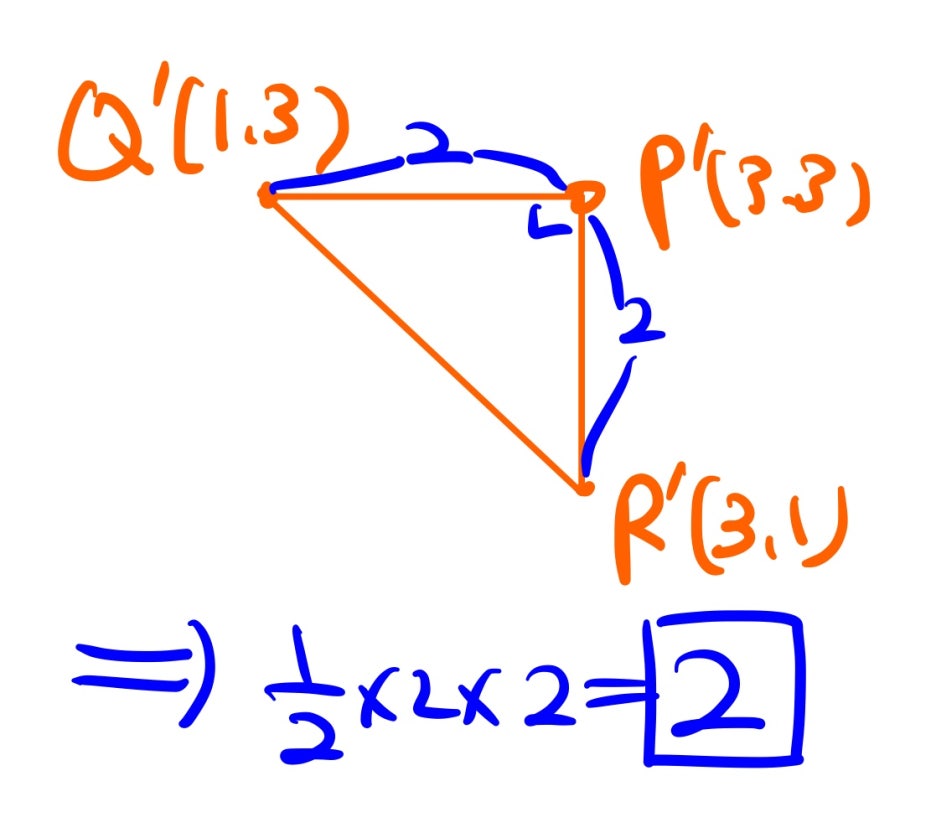
이제 삼각형의 넓이가 최소인 경우를 생각하면 되는데, 계산의 편의를 위해 저는 다음과 같이 평행이동을 했습니다.
평행이동을 해도 삼각형의 넓이는 변하지 않으니 PQR=P'Q'R'이겠죠?


그런데 P'Q'R'의 넓이가 최소가 되는 것은 점 P'에서 선분 Q'R'에 내린 수선의 길이가 최소일 때 입니다. 왜냐하면 이것이 직각이등변삼각형이기 때문입니다!ㅎㅎ


a=3일 때, 삼각형 P'Q'R'의 넓이가 최소이므로~ 이때 넓이를 구하면 되겠죠? 따라서 답은 다음과 같습니다.

기계적으로 문제와 그 풀이를 암기하는 방식으로 공부한 학생이라면 위 세 문항에서 크게 당황 했을 수도 있을 것 같습니다. 하지만 위의 풀이처럼 차근차근 풀면 "[과천중앙고] 2023년 1학년 2학기 기말고사"도 별로 어렵지 않죠?
기계적으로 문제 풀이를 하는 학생을 우수한 학생이라고 생각하는 대학은 없습니다. 배운 것에 근거해서 논리적으로 문제를 해결함으로써 실력을 쌓아나감으로써 우수한 학생이 된다면, 최상위권 대학에서도 여러분을 선발하고자 노력할 거에요. 그러니 그냥 열심히'만' 공부하지 말고, 실력이 쌓이는 방법으로 노력하길 바랍니다!
다음은 실력이 쌓이는 공부 방법에 대한 포스팅 및 전자책 링크입니다.
1. 고난도 문항 치트키 1
2. 고난도 문항 치트키 2
4. 서울대 박사가 알려주는 수학의 비밀 - 첫 번째 비밀 : 집합
5. 서울대 박사가 알려주는 수학의 비밀 - 두 번째 비밀 : 명제
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-
피부도 좋아지고 아침에 잘 일어나짐 ㄷㄷ
-
ㅈㅉㄴ
-
입시알못인데고대공대가능?ㅈㅂ
-
정승제t 개때잡으로 진도 나갈건데 내년꺼 들으면 너무 늦어질거 같아서 이번년도껄로...
-
나같은 허수는 헌신짝
-
고2 자퇴생입니다! 지금 수1, 수2, 확통 하고 있는데 너무 어려워서요.. 모고는...
-
특히 미니의대에 병원도 탄탄하지 않은데 증원이 터무니 없이 많은 곳(대가, 동국,...
-
오르비언중에 한명이 18
내 실친같아서 조금 무서워짐
-
요새 늙어서 그런가 잘 안 일어나네요...
-
영어 성적 변화 13
78-95-97 수능때왤케잘봤지 쓸모도없는데
-
화작 백분위 96 확통 백분위 85 영어 2등급 한국사 1등급 동아시아사 백분위...
-
호날두일생쓰는거임 성경처럼
-
4월 5월에 가려고 했는데 힘들려나요?
-
6에서 7프로 아닐까? 작수보다는 쉬웠고 9평보다는 어려웟는데
-
나 3개가능핳듯 ㅎㅎ
-
근데 동사따위를 칼럼 쓸 가치가 있을까...
-
주사가 뭐에오 9
저는 기억 안나는데 ㅎ헤헤헤 웃으면서 옆에 사람들한테 자꾸 앵기고 기댄다네요.....
-
요즘따라 왜 저런 게시물이 자꾸 메인을 가며, 의대생들 왜 자꾸 긁나요?...
-
모든 기전력 크기와 저항값은 각각 V, R로 동일하다. 특정 저항 내에 흐르는 전류...
-
맥주는이미 준비완료
-
복권 되면 그 깊고도 넓은 은혜 잊지 않겠음
-
참고로그런좋아함은아닙니다 그래서기분이좋네요
-
작년껀 잘 기억 안나는데 6모 2컷 9모 3등급 수능 83점 이때도 83점이...
-
영어성적 2
6모 88 9모 100 수능 98
-
야 다들 잘자라 6
난 애니보러갈거다 좀 박력있었나
-
진짜 겨울이란 건데 그럼... 앞으로 존나 춥겠다
-
2306 1 2309 1 2311 1 2406 1 2409 1 2411 1 수강생의...
-
ㅇ
-
연대 메디컬 성적 띄우고 행복하게 치얼업 보는 게 꿈이었는데… 걍 이제 유튜브...
-
내옆에는 다쓴 휴지뭉치 밖에 없네....
-
서성한 가능한가요..??
-
아 먼가 두껍고 보드보들하고 따뜻한 잠옷 사고 싶다는 생각 들었는데 11
차피 며칠 입을수 없다는 사실이 떠올라버림 ㅠㅠ
-
힘들까요..? 어디까지 지원 해볼만 할지 궁금해요..!
-
영어1맞고가면배가아프기때문
-
오 4
블라됐다!
-
요번에 혼자 알바하면서 반수했다는데 대박남. 전적대가 한의대인데 의대 성적 받아서...
-
사문 옛날 도표기출 풀때 ? 이게 왜 어렵다는거지 생각들면 경제 하면됨 무조건 고득점 간응
-
궁예질 하는 중 0
EYE IS ONE
-
짧다면 짧고, 길다면 긴 2년이란 시간 동안 짝사랑했다 2학년 여름 어느 날,...
-
경제사문 만백 99 나오는거 아니겠지 아
-
물론 칼럼올릴 실력도 아닌것같긴 해요.. 네
-
22도 어디가쒀
-
진학사 1
진학사 지금 나오는 대학별 환산점수가 사과탐 가산점 반영한 점수인가요..?? 너무...
-
69수 영어변화 5
6모 75 9모 71 수능 85 GGB 형님 감사합니다
-
사문 44 45 47(84 92 98예상) 한지 42 42 48(9초반 80...
-
언제든 나가서 개원할 수 있으니 자유롭다 (O) (대부분 전문직 공통) 개원의는...
-
무휴반 주의사항 0
반수한다는 걸 티내면 안됨.. 이해하는 사람들도 있겠지만 티가 나면 알게 모르게...
-
법적으로금지해야..
-
질받 8
야해요




























































아, 참고로 14번 문항은 오류입니다. (k=-5이면 상수함수가 돼서 ㄱ, ㄴ, ㄷ가 모두 거짓이 됩니다^^;;) 집합에서 구별법을 공부해야 한다고 강조했는데~ 분수함수인지 아닌지 구별하는데 신경을 안 쓴 것이 오류의 원인이 된 듯 합니다.