무브

오르비

아톰

내 태그

내 태그 설정

입시
학습
생활
클럽
직업·취업
Epioptimus
Centurion

Cantata [348885] · MS 2010 · 쪽지

2022-12-06 19:59:41
조회수 27,249

수학 예상 최종등급컷

게시글 주소: https://cuttingedge.orbi.kr/00060080119

1. 미적분 예상 확정 등급컷


미적분 1등급 커트라인이 84일 확률과 85일 확률이 모두 존재하는 상황에서


이번에는 만점표준점수를 생각하면서 어느쪽이 더 타당한지 생각해보려 합니다.


다음은 현재 메가스터디의 예상등급컷입니다.





85점 표준점수 133점, 76점 표준점수 126점, 65점 표준점수 118점


과 같이 원점수 구간 대략 10점당 표점 증발이 2~3번씩 일어나는것을 보니


85점에서 100점까지는 3~4번정도는 일어나서 


만점표준점수를 144~5점으로 예상하고 있는 것 같습니다.


그런데 작년 수능 만점표준점수는 147점이었습니다.


올해 수능이 작년 수능보다 전체적인 정답률도 더 낮고,


준킬러~킬러 라인도 더 어려웠는데 만점표준점수가 더 낮은 것은 이해되지 않습니다.


따라서 저는 적어도 147점 이상이라 생각하구요.


그리고 4등급 커트라인은 51점인데 표준점수가 107점으로 되어있습니다.


작년 수능도 4등급 커트라인이 51점이었는데 표준점수는 106점이었구요.


다시말해서 올해 평균점수를 작년 수능에서보다 낮게 잡고 있다는 것이죠.


작년 수능 평균은 44점이었는데, 


올해 수능 평균은 저 표에서 계산해보았을 때 42점정도로 보고 있습니다.


전체적인 정답률이 더 낮은 것을 반영한 결과인 것 같은데요.


그런데 저는 평균점수가 거기서 2점이나 더 떨어질까 하는 의문이 들었습니다.


올해 작년보다 전체적인 정답률이 떨어진게


4~9등급인 학생들에 의한 것이 아니라


1~3등급 학생들에 의한 것이라고 생각했기 때문입니다.


게다가 평균이 더 낮음에도 불구하고 만점표준점수까지 더 낮으면 표준편차는 훨씬 크다는 것인데,


저는 작년 수능에 비해 학생들의 성적대가 더 다양하다고 느끼지 못했습니다.


작년보다 준킬러~킬러 라인이 어려워졌으니, 고득점을 하기 어렵고 평균에 가깝게 몰리는 것이 당연하죠.


즉, 학생들의 성적이 작년보다 다양하지 못할 것입니다.



이러한 종합적인 의문점들을 해소하고자,


저는 올해 수능 평균을 44점으로 잡고,


만점표준점수가 148점이 되도록 표준편차를 조절하여


원점수-표준점수-백분위-등급 테이블을 만들어보았습니다.




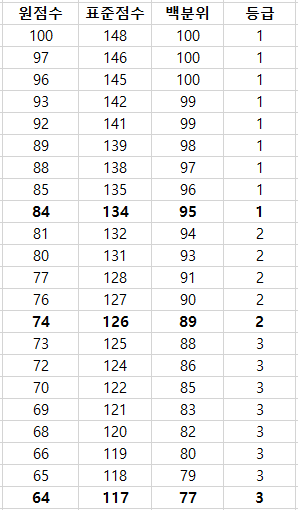
1등급 커트라인이 84점인 경우:




1등급 커트라인이 85점인 경우:



                                               




*1등급 커트라인이 84점인 경우 96점 백분위를 100, 


 1등급 커트라인이 85점인 경우 96점 백분위는 99로 설정하였는데


 이는 96점 백분위가 99일 확률과 100일 확률이 거의 반반임을 상징적으로 나타낸 것입니다.


 1등급 커트라인이 84점일 때 96점 백분위가 100이 나오고,


 1등급 커트라인이 85점일 때 96점 백분위가 100이 안나온다는 뜻은 아닙니다.




여전히 이 두 성적분포가 모두 가능해보이긴 한데,


그래도 저는 작년 수능처럼 1, 2, 3등급 커트라인 간격이 고를 확률이 더 크지 않나 하구요.


또한 2등급 커트라인 표준점수가 127점보다는 126점이 더 일반적이라 생각하여 


1등급 커트라인 84, 2등급 커트라인 74, 3등급 커트라인 64


를 밀어봅니다!





2. 확률과 통계 예상 확정 등급컷


저는 미적분과 확률과 통계 등급컷 차이를 꽤 정확히 추정할 수 있는 공식을 찾아냈습니다.


물론 귀납적인 것이고 우연성이 강한데, 지금까지는 평가원에서 모두 적중하고 있어서 소개합니다.


(수능에서 저격당하기 전 찍기특강 같은 느낌이라 보시면... 언제 틀릴지 모르지만 지금까지는 맞아온...)


다음 표는 22.6평, 23.9평, 23.6평, 23.9평 미적분, 확통의 문항별 정답률 및 평균을 나타낸 것입니다.





맨 아랫줄에 '보정평균'이라는 것이 있는데,


여기서 미적분의 평균은 그대로 쓰고, 확률과 통계의 평균은 1.16배를 하여 씁니다.


그리고


(확률과 통계의 보정평균)-(미적분의 보정평균)


의 값을 2로 나누면 


확률과 통계가 미적분에 비해 손해보는 점수가 산출되는데요.


그 결과


22학년도 6평은 6점, 9평은 7점,


23학년도 6평은 6점, 9평은 3점이 산출되고


이는 실제 결과와도 일치했습니다.



그런데 문제는 작년 수능입니다. 






위에서와 같은 방법으로 보정평균을 구했더니 오히려 확률과통계가 살짝 더 낮았는데요.


(59.74-60.5)/2의 값을 소수 첫째자리에서 반올림하면 그래도 0이라서


미적분 등급컷과 동일할 것으로 예상을 했었는데,


실제로는 확률과 통계가 미적분보다 3점이나 손해보는 결과가 나왔었습니다.


따라서 보정평균을 낼 때 확률과 통계에 1.16이 아니라 더 큰 값을 곱해야할 것으로 생각을 했고,


적당한 값을 찾다보니 최소 1.28은 되어야한다는 사실을 알 수 있었습니다.





이 경우 (65.92-60.5)/2의 값이 대략 3이 나오기 시작합니다.



그렇다면 평가원에서는 1.16을 곱하면 되고, 수능만 1.28을 곱하는 것이 맞는 걸까요?


아니면 유독 작년 수능만 확률과 통계가 억까를 당한 것일까요?


결론을 내릴 수 없어서 두 가지 경우 모두 생각해보았는데, 


우선 1.16을 곱한 경우는 다음과 같았습니다.





(62.35-59.375)/2의 값을 계산하면 대략 1~2점 정도 손해보는 결과가,


(수능을 제외한 최근 4번의 평가원 시험에서는 이 결과가 모두 맞았음.)


작년 수능처럼 보수적으로 1.28을 곱한 경우





(68.8-59.375)/2의 값을 계산하면 대략 5점 정도 손해보는 결과가 나오기도 합니다.


1~2점이랑 5점은 차이가 너무 많이 나서 어느쪽을 선택할 지 고민이 되었는데,


작년 수능 확률과 통계 등급컷이 높았던걸 생각하면 5점에 더 가깝지 않을까 생각했습니다.


결론적으로 확률과 통계가 4점 손해보는 등급컷을 산출해보았습니다.







3. 기하 예상 확정 등급컷


기하도 앞서 확률과 통계에서처럼 정답률을 보정하여 추정하는 방식을 찾아보긴 했는데,


정확도가 확률과 통계에 비해서는 조금 떨어집니다.


그래서 자세한 과정은 여기에 적지 않고 결과만 말씀드리면, 


기하가 미적분보다 4~5점을 손해보는 결론을 내렸습니다.


미적분 1등급 커트라인을 84.5점으로 가정하고, 이보다 4.5점을 손해본다고 가정해서


1등급 커트라인이 89점이 되도록 등급컷을 산출해보았습니다.





0 XDK (+0)

  1. 유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.

Cantata [348885]

쪽지 보내기

글쓰기
오르비 1356291번째 회원 가입
ddna
1,422,072 건의 게시물이
블록체인에 디지털 공증되었습니다.
901,751
497,321
22,267
574
159

오르비 캐스트

2026 수능D - 349

오르비 플레이

오르비 RARE

오르비 과외시장
Move
our corporate site
Orbi Class
on-line classes
Atom
educational books & resources
Gae9
humor and fun

© 2000-2024 Move Inc.

orbisoptimus (v17-7e2515)